“Windmills in my mind
spinning silky webs serene
sensuous colors…”
Those are a few lines from the poem “Windmills in My Mind” by poet Melanie Bishop which describes the beautiful appearance of windmills.
Huge and tall windmills are relatively new creatures for people who live in big cities. Several months ago when I was visiting the Chongming Island, an ecological island near urban Shanghai, I was attracted by those windmills standing high up the sky. When there was a burst of wind, the windmills start to rotate slowly and gently. And every time it rotates, I was fascinated by that. I don’t know why. But sometimes there is no need for a reason.
A windmill is a mill that converts the energy of wind into rotational energy by means of vanes called sails or blades, according to Wikipedia. From Physics’ perspective, a windmill converts the kinetic energy of the wind from the air to the kinetic energy on its blades so that they move. The blades then rotate the turbine and finally kinetic energy is transferred to electrical energy by the generator. When the windmill rotates, it does a centripetal motion. Normally, the faster it rotates, the more kinetic energy the blades have (we does not consider the case when the wind speed is too high since then it will stimulates its protection mechanism).
Windmills have a very long history. Centuries ago, windmills usually were used to mill grain and pump water. Modern windmills are usually used to produce electricity. Therefore, windmills are an important sign which shows that human beings make good use of renewable and green energies.
However, from Physics lessons we learnt from school, I find that wind power has a lot of limitations. For example, the power output is highly affected by various environmental factors, such as the wind speed. In addition, even though we assume that we have very stable wind speed, the wind direction changes all the time, and will affect the power output of the windmill.
THE RESEARCH QUESTION
According to the knowledge in Physics lessons, the output of wind power is only affected by two factors: the area of the blades and the wind speed. However, in real world, not all wind comes 90 degrees directly into the blades, and the varying wind direction (or the angle the direction of the wind deviates from 90 degrees) must also have an impact on the rotational speed, or the power output of the windmill. Therefore, my research topic is “What is the relationship between the wind direction in horizontal and the rotational speed of a windmill?”. The topic is very worthwhile since we need to decide the location of a wind power station and the direction a windmill faces to, according to the most common wind direction in that specific area. If we wish to build an efficient wind power station, we have to investigate how will the wind direction affect the power of the windmills.
EXPERIMENTAL VARIABLES
Since I only want to investigate how the angle (wind direction) affects the rotation speed, I have to eliminate other factors that may influence the results of the experiment. For example, the original speed of the wind and the distance between the wind origin and the blades must be kept constant. In addition, since we only wish to change in the wind direction in horizontal, we need to make sure the wind direction does not change in vertical. Other factors such as the air resistance and the external temperature must also be kept unchanged.
In this experiment, the independent variable is the angle the wind direction deviates from 90 degrees in horizontal. The dependent variable is the speed of rotation of the blades on a windmill. I change the independent variable, the angle (direction), and examine how the dependent variable, the rotational speed, changes in response to the independent variable.
EXPERIMENTAL DESIGN
The purpose of this experiment is to test the relationship between the angle the wind direction deviates from 90 degrees in horizontal and the rotational speed of the windmill.
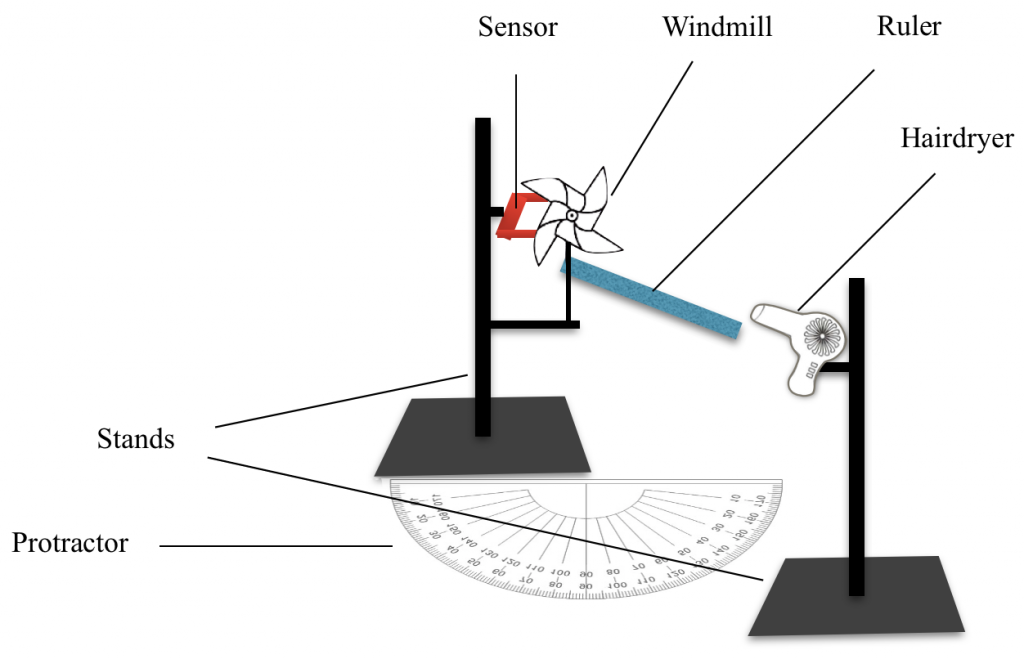
I prepare all the following equipments needed to finish this experiment:
- To make sure the original speed of the wind is constant, I need a hair drier and always set it to the LOW power output. (Though I do not know the exact wind speed, it does not matter because the change in wind speed is not considered in this experiment)
- To measure that the the distance between the wind origin and the blades is constant, I need a 1-meter-long ruler with clear scales on it.
- I need a motion sensor to test the rate of rotation of the blades on the windmill.
- A big protractor is required to measure the angle between the wind origin and the blades.
- Two retort stands are needed to fix the positions of all the equipments.
- And of course, I have a colorful toy windmill with four blades.
The draft of the graph of my experiment is the following:
EXPERIMENTAL PROCESS
- First, I attach the windmill to the first resort stand, and fix its position including its height.
- Then I setup the sensor on the first resort stand and make sure that the four blades of the windmill can all pass through the sensor when they rotate without touching the sensor.
- After that, I attach the ruler to the first stand in the horizontal direction. The ruler must make a right angle with the stick of the stand.
- In addition, I need to make sure the front opening of the hair drier (where the wind comes from) always perfectly points at the center-point of the four blades even though I change the wind direction, so that four blades can receive equal amount of kinetic energy.
- Then I attach the hairdryer to the second resort stand, fix its position tightly including its height, and make sure that it cannot be moved in all directions.
- Finally, I power on the hair drier, set it to LOW power to make sure the wind speed is unchanged, and change the angle according to the readings on the protractor by moving the second stand around. Each time I change the angle, I make sure the distance between the hairdryer and the blades keeps constant at 40 cm by using the readings on the ruler.
- The different angles I pick are 0, 20, 40, 50, 60, 80 and 90 degrees.
- I measure the rotational speed 3 times for the same wind direction (angle), and then use the average to plot the data. Repeating experiments makes my data and results more accurate.
DATA COLLECTION
The sensor is connected to the Verner Lab Pro interface and then is connected to the computer. The Logger Pro software automatically senses the motion sensor and displays graphs axes of rotational speed against time on the screen in the form like this:
The following table shows the results of the experiment:
| Angle (degrees) | Rotational speed (ms-1) – Trial 1 | Rotational speed (ms-1) – Trial 2 | Rotational speed (ms-1) – Trial 3 |
| 0 | 0.7047 | 0.7089 | 0.6719 |
| 20 | 0.6332 | 0.6671 | 0.6557 |
| 40 | 0.5463 | 0.5299 | 0.5632 |
| 50 | 0.4593 | 0.4822 | 0.498 |
| 60 | 0.4247 | 0.4562 | 0.4246 |
| 80 | 0.2536 | 0.2655 | 0.2312 |
| 90 | 0.1317 | 0.1202 | 0.1035 |
DATA PROCESSING
Mean rotational speed = (V1 + V2 + V3) ÷ 3
For example, the mean rotational speed of trial 20° is:
(0.6332 + 0.6671 + 0.6557) ÷ 3 = 0.6520 ms-1
Uncertainty = (Vmax – Vmin) ÷ 2
For example, the uncertainty of trial 40° is:
(0.5299 – 0.5632) ÷ 2 = 0.0167 ms-1
| Angle (degrees) | Mean rotational speed (ms-1) | Uncertainty (ms-1) |
| 0 | 0.6952 | 0.0185 |
| 20 | 0.6520 | 0.0170 |
| 40 | 0.5465 | 0.0167 |
| 50 | 0.4798 | 0.0194 |
| 60 | 0.4352 | 0.0158 |
| 80 | 0.2501 | 0.0172 |
| 90 | 0.1185 | 0.0141 |
DATA ANALYSIS
The mean rotational speed (ms-1) is graphed against the angle (°) in the following diagram:
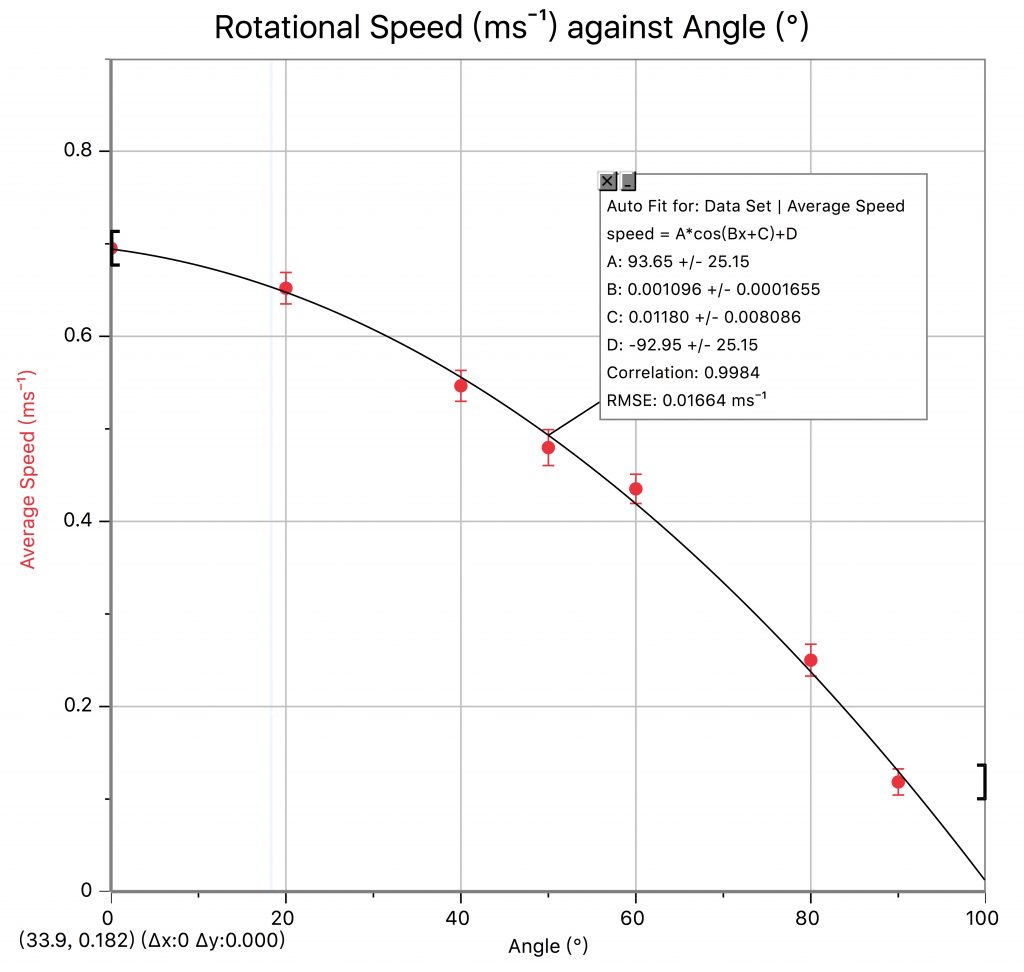
I try several different kinds of function relationships to fit the data, and find that a cosine function fit the data the most perfectly because the curve is able to cross all the error bars of the data on the graph. The correlation is 0.9984, which means that the data fits this curve very well.To prove that there is a cosine relationship between angle and rotational speed, the cos(mean speed of rotation) or cos(V) is now also graphed against the angle (°) in the following diagram:
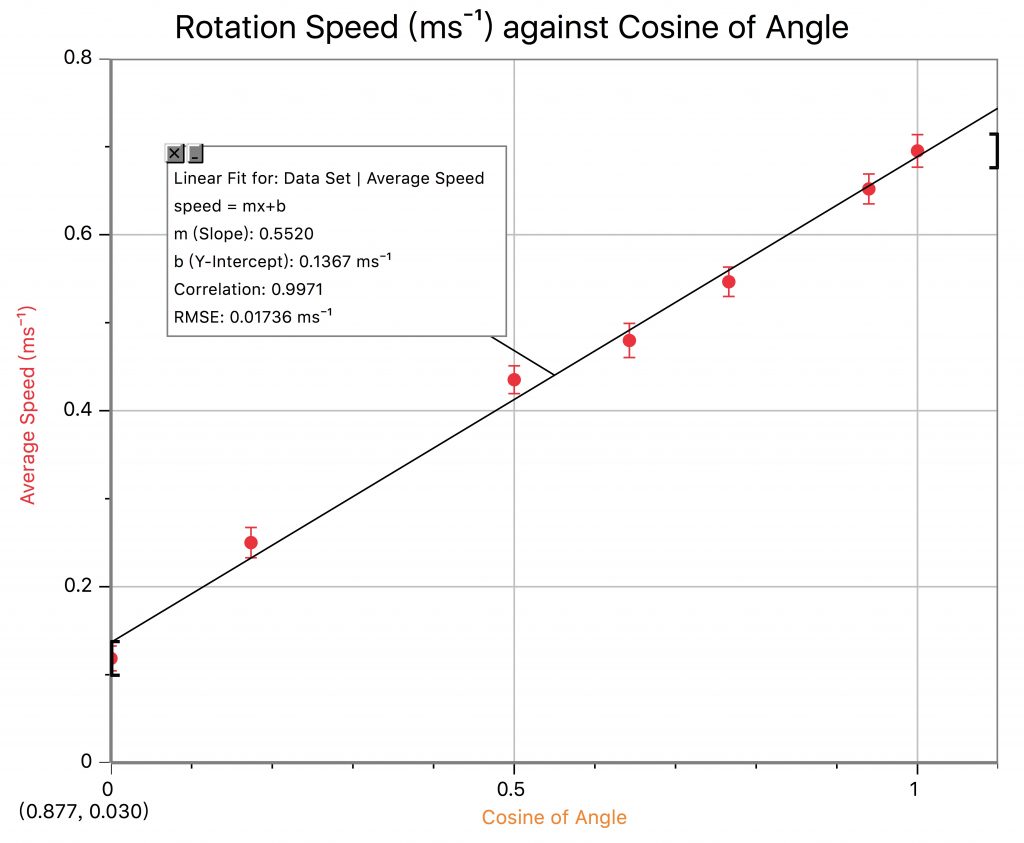
From the graph below, I find that the cosine of rotational speed is proportional to the angle which deviates from 90°, which proves that my judgement is correct. Therefore, the rotational speed of the blades does have a cosine relationship with the angle.
Using the findings from the graphs, I also use the following methods to further prove and illustrate the cosine relationship between rotational speed and angle.
From the knowledge I learnt from Physics lessons, I know that:
P = 0.5ρAv3
(Where P is the power output of the windmill, ρ is the air density, A is the area of the blades, and v is the wind speed.)
However, in this formula of power (or rotational speed, which is the same in this case), it is assumed that the wind comes 90 degrees directly into the blades, which is not always possible.
In the graph below, V1 is the real wind speed where there is a deviation, V2 is the v in the formula P = 0.5ρAv3, and α is the angle that deviates from 90° (which is the independent variable in my experiment). Therefore, it is found that if there is a deviation from 90°, only a part of the wind speed will be useful in pushing the blades moving around.
And the relationship between V1 and V2 can be derived by:
cos(α) = V2/V1
V2 = V1 cos(α)
And this illustrates why there is a cosine relationship between rotational speed and angle.
CONCLUSION
From the first graph plotted, we can deduce that the rotational speed of a windmill has an cosine relationship with the angle of the wind which deviates from 90 degrees. As the angle of the wind which deviates from 90 degrees increases, the rotational speed of the windmill decreases.
If we graph the rotational speed against cosine value of angle, we can find that the speed has a linear relationship with cos(α). This also proves that he rotational speed of a windmill has an cosine relationship with the angle of the wind which deviates from 90 degrees.
EVALUATION
Though the data does show an exponential relationship, the data is not accurate enough. When we are collecting the data of rotational speed, we find out that for the same angle, the rotational speed fluctuates a lot. Every trial has a large difference from the other ones for the same angle. Because originally I did not have any equipment to fix the position of the hair drier, I had to do that by man power. This meant that we were not able to make sure that the front opening of the drier (where the wind comes from) directed precisely at the mid-point of the four blades. In addition, human hands may shake a lot during the experiment. Therefore, I could not make sure that the direction of the wind was always constant. The rotational speed may change due to the change in wind direction. After I realized this problem, I used another stand to fix the position of the hairdryer, and the situation became much better. In addition, since the air conditioner was on in the lab, the data could be affected a little bit.
IMPROVEMENTS
I can make some improvements to make the data in the experiment more precise or complete:
- I can do the experiment in a perfectly windless indoor room to avoid some fluctuations because of the change in strength of airflow.
- I can also do further experiments in the future to find how other factors influences the rotational speed of the windmill. For example, I can investigate the distance from the wind origin to the blades, or the direction changes in vertical instead of horizontal.
